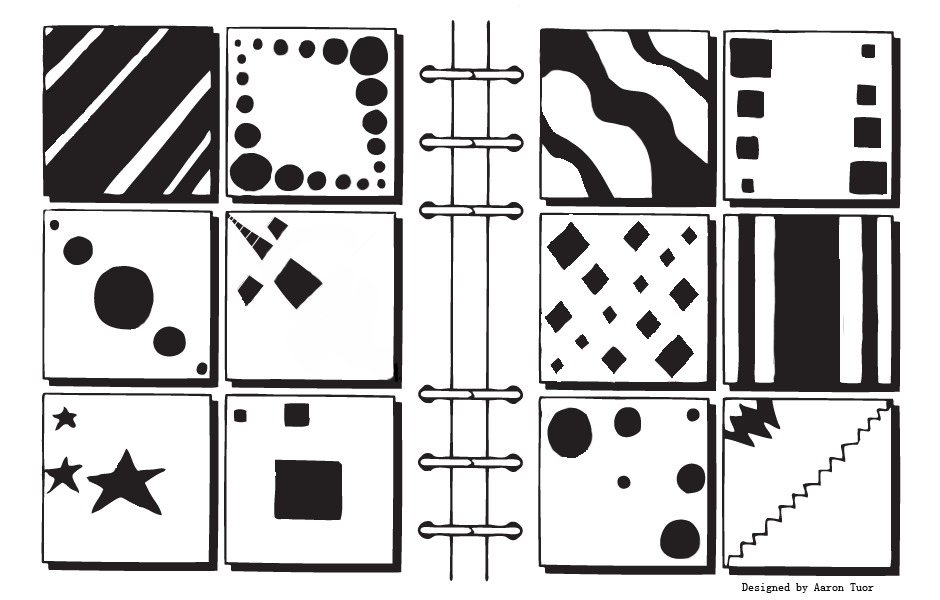
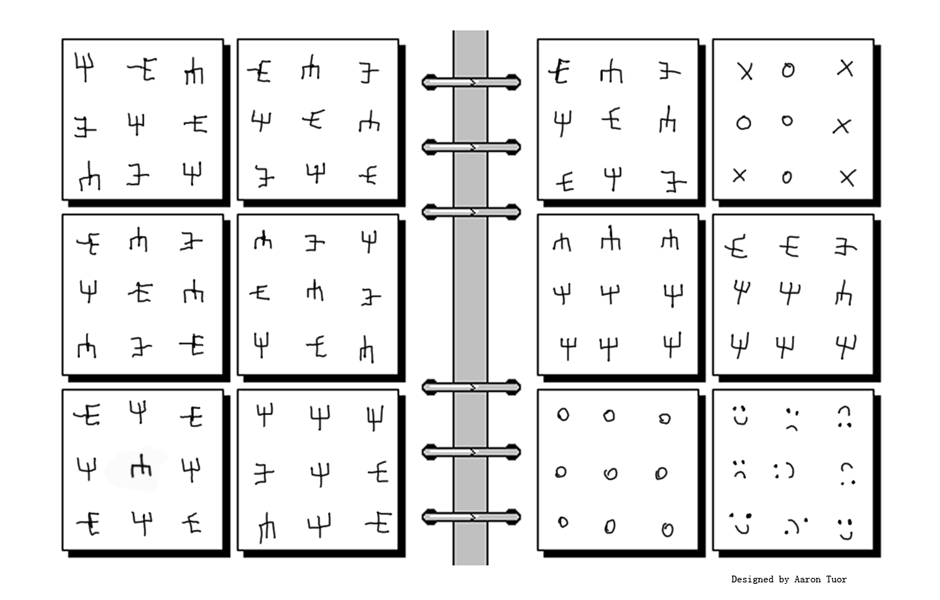
Bongard problems are a type of geometric puzzle which first appeared in the appendix of the book Pattern Recognition (1967) by Russian scientist M. Bongard. These problems consist of two sets of six drawings. The drawings on the left page of the Bongard problem conform to a pattern which the drawings on the right page do not. The goal is to figure out the pattern of the drawings on the left page. These puzzles merit some attention not only because they are fun to do, but also for the opportunity to reflect on the process of their production and solution. In solving Bongard problems one may think of several patterns before actually discovering a pattern which works. This process helps to define features which are not essential to the pattern. But how do people make the leap from "what the pattern isn't" to "what the pattern is"? If confronted with a previously recognized pattern a person may be guided by such a process of elimination to the goal of a solution. What about patterns a person has never encountered before? What happens the first time a person encounters and recognizes a new pattern? In an effort to answer these types of questions, Harry Foundalis, as part of his doctoral research on fundamental principles of human cognition, developed a computer program, Phaeco, designed to solve Bongard problems in a humanlike fashion. To learn more about his research visit his website (here) where you can also find a collection of over 200 Bongard problems.