Koch Snowflake Inverted Koch Snowflake

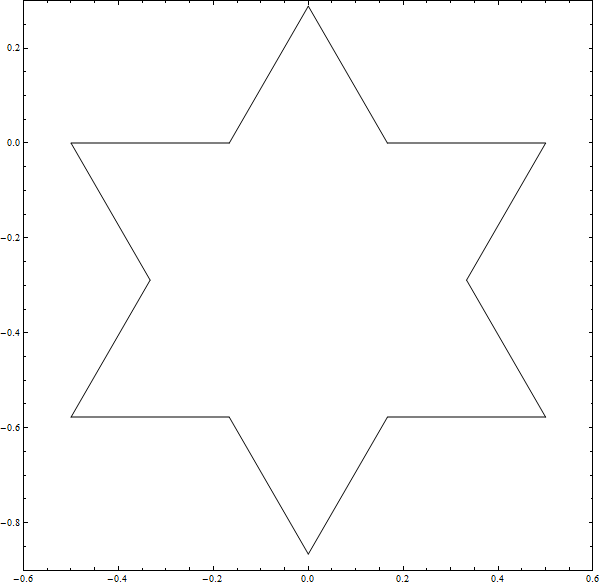
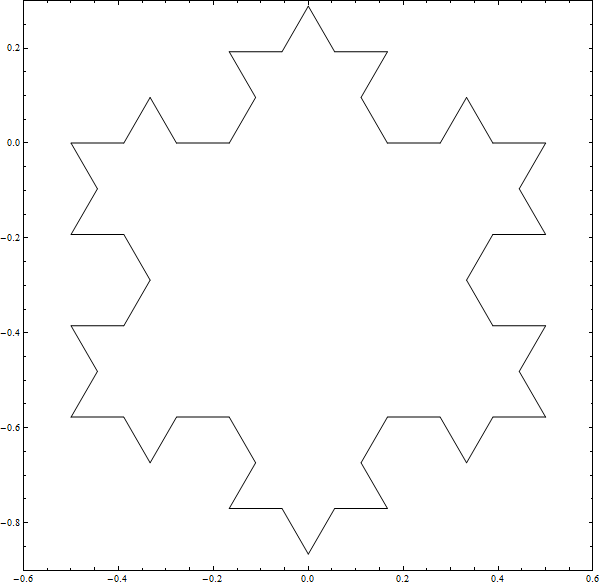
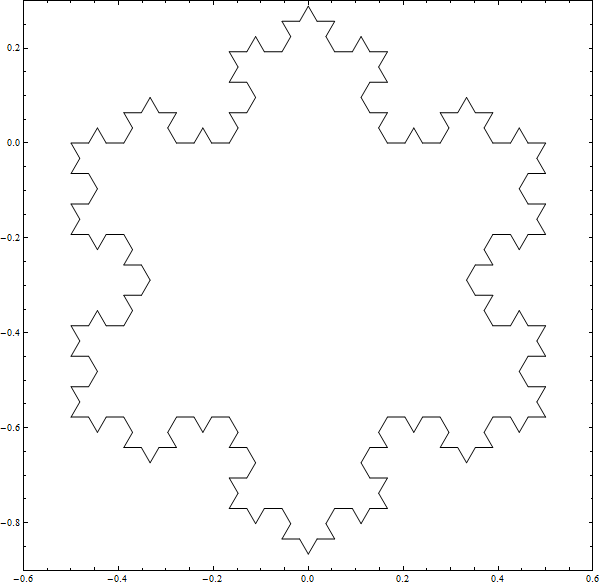


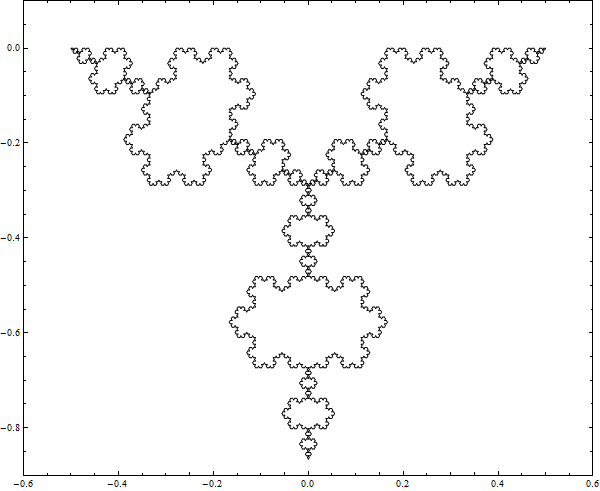
Below are demonstrations of constructing the Koch Snowflake and the Inverted Koch Snowflake. To make the Koch snowflake you start with an equilateral triangle. In the first iteration you add equilateral triangles for each of the sides. These added triangles have sides of length 1/3 the length of the original triangle, and they are centered on the sides of the original triangle. Then do the same thing for all the new triangles, and keep doing this until you run out of time. In the limit you end up with a geometric figure which has infinite perimeter and finite area.
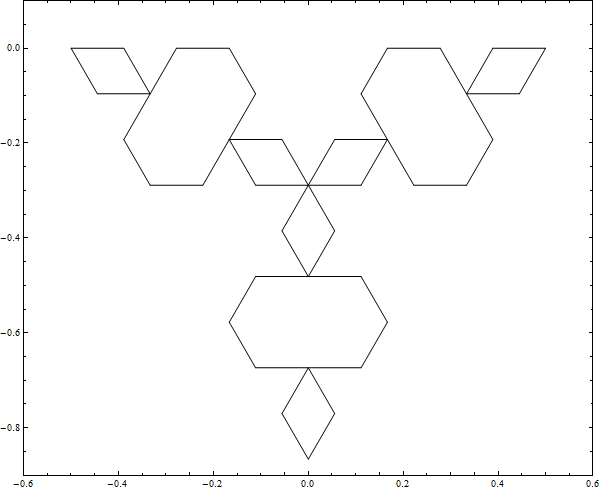
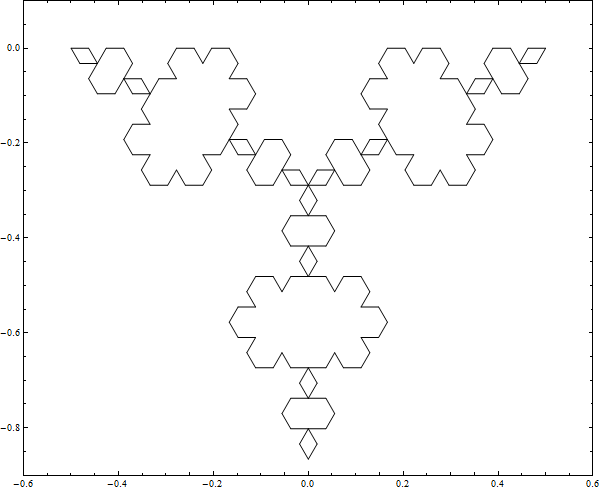
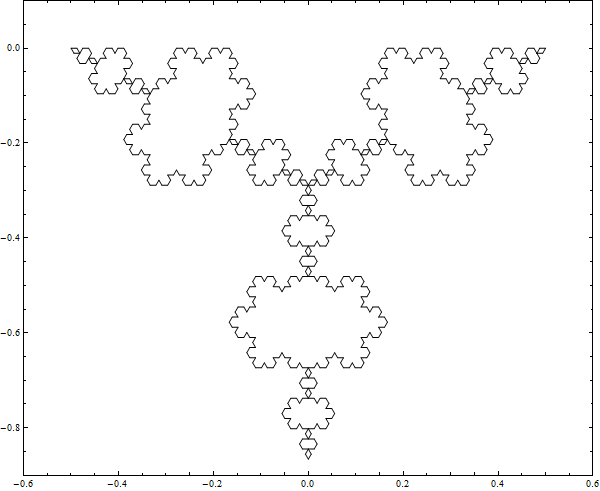
The Inverted Koch Snowflake is just like the regular Koch Snowflake except that you subtract triangles from the original triangle. Below are images of 6 iterations building the inverted and regular Koch Snowflakes alongside each other.












From inspection of the pictures and reflection upon the algorithms you can see that the area being added to the Koch snowflake is the same amount of area that is being subtracted from the inverted Koch snowflake. You may also be able to convince yourself that at any iteration the Koch and inverted Koch should have the same perimeter. I mentioned that the Koch snowflake has a finite area. There are well known proofs involving the sum of an infinite series that demonstrate this. I like Salmon Kahn's demonstration.
These pictures suggest an alternate way of establishing a finite area for the Koch snowflake using geometric facts and the principle of induction. We won't get an exact figure for the area but we can bound it between one and two times the size of the area of the original triangle. The idea goes as follows:
True:Since the area added to the Koch is the same as the area being removed from the inverted Koch, and the triangles which both algorithms begin with are the same, if we always have room in the inverted Koch to remove what we need, then the Koch will never grow to be twice it's original area.
Here is how we can prove the if in previous statement, that we always have room in the inverted Koch snowflake to remove what we need.
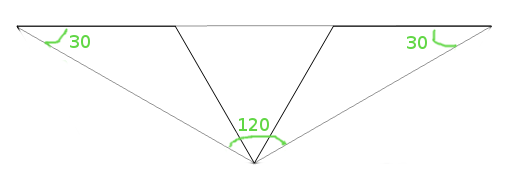
FactFirst, let's show that a 30, 30, 120 triangle has room to remove an equilateral triangle a third the length of the longest side and centered at the middle. I'll call such a removal a 30, 30, 120 equilateral triangle removal procedure. That's as easy as a picture.
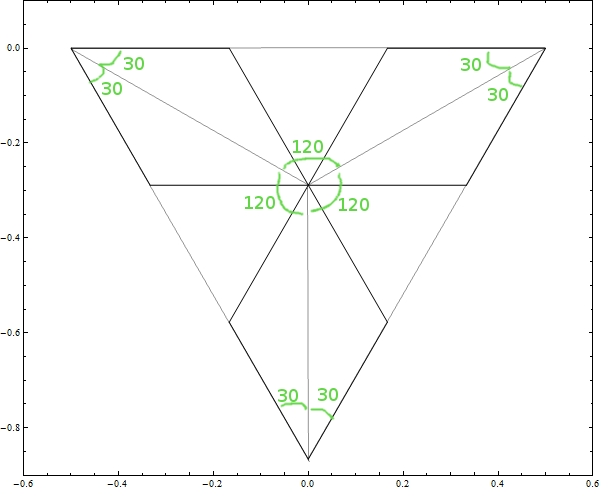
Now we can show that on the first iteration ot the inverted Koch we can express our removal algorithm as a collection of nonoverlapping 30, 30, 120 equilateral triangle removal procedures. The grey lines show the 30, 30, 120 triangles I was mentioning. Since these triangles don't overlap and we are removing from their interiors we can't remove from the interior of another of the 30, 30, 120 triangles. So, we have room.
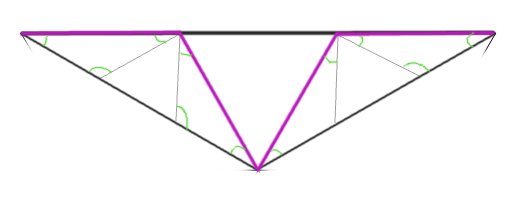
Okay, now suppose that at the k-th iteration we can express the removal algorithm as a collection of nonoverlapping 30, 30, 120 equilateral triangle removal procedures. We just have to show that at the (k+1)th iteration we can do the same and we'll always have room for removal.
Since the 30, 30, 120 triangles at the k-th iteration are assumed to be non-overlapping, if we show the case for one of the 30, 30, 120 triangles then we are done.
In the picture below a 30, 30, 120 triangle is depicted by thick black lines. The removal sides in question for the (k+1)th iteration are depicted by purple lines. The thin black lines show how to make the removal problem into a problem of nonoverlapping 30, 30, 120 equilateral removal procedures. So, we'll always have room to remove from the inverted Koch by its process.
Since the Koch snowflake is symmetrical in the algorithm for its three original sides, if we add the production of perimeter for one side together for infinity it will diverge as well as the other two. Since the algorithm is the same for the smaller sides that are produced, because of the recursive nature of the algorithm, then these ostensibly smaller sides must diverge as well. So in the limit any portion of the Koch snowflake, however small, must have infinite length.